二叉树的遍历java实现

1 二叉树遍历方法

二叉树深度优先遍历（配合leetcode进行练习）
- 前序遍历： 144. 二叉树的前序遍历
- 后序遍历： 145. 二叉树的后序遍历
- 中序遍历： 94. 二叉树的中序遍历
二叉树广度优先遍历
- 层序遍历：102. 二叉树的层序遍历

2 深度优先遍历

2.1 递归解法

2.1.1 通用框架

public List<Integer> mlr(TreeNode root){
    List<Integer> res=new ArrayList<>();
    helper(res,root);
    return res;
}

2.1.2 前序遍历

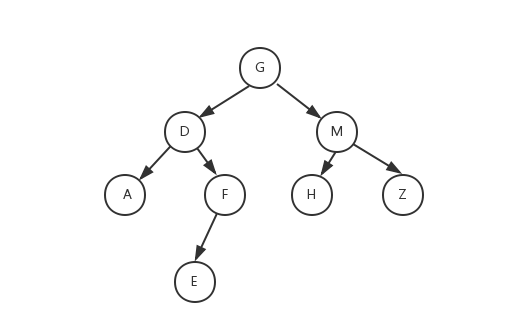
访问顺序：先根节点，再左子树，最后右子树；上图的访问结果为：GDAFEMHZ。

class Solution {
    //递归法
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        preorderTraversalHelper(root, list);
        return list;
    }

    private void preorderTraversalHelper(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }

        list.add(root.val);
        preorderTraversalHelper(root.left, list);
        preorderTraversalHelper(root.right, list);
    }
}

2.1.3 中序遍历

访问顺序：先左子树，再根节点，最后右子树；上图的访问结果为：ADEFGHMZ。

class Solution {
    //递归解法
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        inorderTraversalHelper(root, list);
        return list;
    }

    private void inorderTraversalHelper(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }

        inorderTraversalHelper(root.left, list);
        list.add(root.val);
        inorderTraversalHelper(root.right, list);
    }
}

2.1.4 后序遍历

访问顺序：先左子树，再右子树，最后根节点，上图的访问结果为：AEFDHZMG。

class Solution {
    //递归解法
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        postorderTraversalHelper(root, list);
        return list;
    }

    private void postorderTraversalHelper(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }

        postorderTraversalHelper(root.left, list);
        postorderTraversalHelper(root.right, list);
        list.add(root.val);
    }
}

2.2 迭代解法

2.2.1 前序遍历

我们使用栈来进行迭代，过程如下：

初始化栈，并将根节点入栈：stack.push(root);
当栈不为空时：
- 弹出栈顶元素： root = stack.pop();，并将值添加到结果中res.add(root.val);
- 如果 node 的右子树非空，将右子树入栈；
- 如果 node 的左子树非空，将左子树入栈；

由于栈是“先进后出”的顺序，所以入栈时先将右子树入栈，这样使得前序遍历结果为 “根->左->右”的顺序。

此时你能得到的流程如下:

class Solution {
    //迭代解法
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        //1.初始化栈，将根节点入栈
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);

        while (!stack.isEmpty()) {
            //2.弹出栈顶元素，并将值添加到结果中，此时root为弹出后的节点
            TreeNode node = stack.pop();
            res.add(node.val);

            //3.如果 node 的右子树非空，将右子树入栈；
            // 如果 node 的左子树非空，将左子树入栈；因为出栈是后进先出
            if (node.right != null) {
                stack.push(node.right);
            }
            if (node.left != null) {
                stack.push(node.left);
            }
        }
        return res;
    }
}

2.2.2 中序遍历

同理创建一个Stack，然后按左中右的顺序输出节点。
尽可能的将这个节点的左子树压入Stack，此时栈顶的元素是最左侧的元素，其目的是找到一个最小单位的子树(也就是最左侧的一个节点)，并且在寻找的过程中记录了来源，才能返回上层,同时在返回上层的时候已经处理完毕左子树了。
当处理完最小单位的子树时，返回到上层处理了中间节点。（如果把整个左中右的遍历都理解成子树的话，就是处理完左子树->中间(就是一个节点)->右子树）
如果有右节点，其也要进行中序遍历

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        //1.初始化栈
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node = root;

        while (!stack.isEmpty() || node != null) {
            //将该节点的左字数节点全部压入Stack中，当node=null时，说明栈顶元素为最左侧的元素
            if (node != null) {
                stack.push(node);
                node = node.left;
            }else {
                //当栈顶元素为最左侧的元素时，1.栈顶元素出栈，添加到res结果中，2.寻找右节点进行遍历
                node = stack.pop();
                res.add(node.val);
                node = node.right;
            }
        }
        return res;
    }
}

当整个左子树退栈的时候这个时候输出了该子树的根节点 2，之后输出中间节点 1。然后处理根节点为3右子树。

2.2.3 后序遍历

后序遍历的过程为左右中，因此我们的思路为：

前序遍历的过程是中左右。
将其转化成中右左。也就是压栈的过程中优先压入左子树，在压入右子树。
出栈将其添加到list中时，采用add(0, node.val)方法使其在列表中的顺序即为中右左的倒序。

class Solution {
    //迭代解法
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        //1.初始化栈，将根节点入栈
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);

        while (!stack.isEmpty()) {
            //2.弹出栈顶元素，并将值添加到结果中，此时root为弹出后的节点
            TreeNode node = stack.pop();
            //此处巧妙的地方为：将node.val值插入列表时，设置在index=0位置插入，后面的元素向后移位，便可以达到反转遍历顺序的目的
            res.add(0, node.val);

            //3.前序遍历时入栈顺序为右子树先入，左子树后入，因为出栈时左子树能先出，遍历的顺序为中左右
            // 后序遍历需要的顺序为左右中，我们将左右子树的入栈顺序调换后，遍历顺序为中右左，将顺序反转后即为左右中。
            if (node.left != null) {
                stack.push(node.left);
            }
            if (node.right != null) {
                stack.push(node.right);
            }
        }
        return res;
    }
}

2.3 Morris解法

Morris遍历使用二叉树节点中大量指向null的指针，由Joseph Morris 于1979年发明。时间复杂度：O(n) 额外空间复杂度：O(1)

在你阅读以下代码之前，在这边先讲解一下Morris的通用解法过程。

3 广度优先遍历

3.1 层序遍历

3.1.1 迭代解法

广度优先遍历是按层层推进的方式，遍历每一层的节点。题目要求的是返回每一层的节点值，所以这题用广度优先来做非常合适。广度优先需要用队列作为辅助结构，我们先将根节点放到队列中，然后不断遍历队列。

首先拿出根节点，如果左子树/右子树不为空，就将他们放入队列中。第一遍处理完后，根节点已经从队列中拿走了，而根节点的两个孩子已放入队列中了，现在队列中就有两个节点 2 和 5。

第二次处理，会将 2 和 5 这两个节点从队列中拿走，然后再将 2 和 5 的子节点放入队列中，现在队列中就有三个节点 3，4，6。

我们把每层遍历到的节点都放入到一个结果集中，最后返回这个结果集就可以了。时间复杂度： O(n) 空间复杂度：O(n)

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        if (root == null) {
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            //获取当前队列的长度，这个长度相当于 当前这一层的节点个数
			int size = queue.size();
			List<Integer> tmp = new ArrayList<Integer>();
			//将队列中的元素都拿出来(也就是获取这一层的节点)，放到临时list中
			//如果节点的左/右子树不为空，也放入队列中
			for(int i=0; i<size; ++i) {
				TreeNode t = queue.remove();
				tmp.add(t.val);
				if(t.left!=null) {
					queue.add(t.left);
				}
				if(t.right!=null) {
					queue.add(t.right);
				}
			}
			//将临时list加入最终返回结果中
			res.add(tmp);
        }
        return res;
    }
}

文章目录