Leetcode连载 | 数组
移动零
给定一个数组 `nums`,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
1. 必须在原数组上操作,不能拷贝额外的数组。
2. 尽量减少操作次数。
class Solution {
public void moveZeroes(int[] nums) {
if (nums == null) {
return;
}
//使用双指针i,j,用指针i遍历数组,用指针j记录非0元素的下标
int j = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] != 0) {
nums[j++] = nums[i];
}
}
for (int i = j; i < nums.length; i++) {
nums[i] = 0;
}
}
}
重塑矩阵
在MATLAB中,有一个非常有用的函数 reshape,它可以将一个矩阵重塑为另一个大小不同的新矩阵,但保留其原始数据。
给出一个由二维数组表示的矩阵,以及两个正整数r和c,分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。
如果具有给定参数的reshape操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
输入:
nums =
[[1,2],
[3,4]]
r = 1, c = 4
输出:
[[1,2,3,4]]
解释:
行遍历nums的结果是 [1,2,3,4]。新的矩阵是 1 * 4 矩阵, 用之前的元素值一行一行填充新矩阵。
public int[][] matrixReshape(int[][] nums, int r, int c) {
if (nums.length == 0 || (nums.length * nums[0].length) != (r * c)) {
return nums;
}
int row = 0;
int col = 0;
int[][] res = new int[r][c];
//当col==c-1时,矩阵换行
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < nums[0].length; j++) {
res[row][col] = nums[i][j];
if (col == c - 1) {
row++;
col = 0;
}else {
col++;
}
}
}
return res;
}
最大连续1的个数
给定一个二进制数组, 计算其中最大连续1的个数。
示例 1:
输入: [1,1,0,1,1,1]
输出: 3
解释: 开头的两位和最后的三位都是连续1,所以最大连续1的个数是3.
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int count = 0;
int max = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == 1) {
count++;
}else {
max = Math.max(count, max);
count = 0;
}
}
return Math.max(count, max);
}
}
搜索二维矩阵
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例:
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
解题思路
由于矩阵元素从左到右从上到下依次递增,因此我们考虑从矩阵的右上角进行遍历,令**row=0**及**col=matrix[0].length - 1**,在遍历时满足以下条件:
1. 当前元素大于target值时,向矩阵左边遍历,因此**col-=1;**
2. 当前元素小于target值时,向矩阵下面遍历,因此**row+=1;**
3. 当前元素等于target值时,返回**true**
当**row < matrix.length && col >=0**时循环结束,返回**false**
代码
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0) {
return false;
}
int row = 0;
int col = matrix[0].length - 1;
while(row < matrix.length && col >=0) {
if (matrix[row][col] > target) {
col -= 1;
}else if (matrix[row][col] < target){
row += 1;
}else {
return true;
}
}
return false;
}
}
有序矩阵中的第K小的元素
给定一个 n x n 矩阵,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
请注意,它是排序后的第 k 小元素,而不是第 k 个不同的元素。
示例:
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8,
返回 13。
解题思路
思路非常简单:
1.找出二维矩阵中最小的数**left**,最大的数**right**,那么第k小的数必定在left~right之间
2.mid=(left+right) / 2;在二维矩阵中寻找小于等于mid的元素个数count
3.若这个**count**小于k,表明第k小的数在右半部分且不包含**mid**,即**left=mid+1**, **right=right**,又保证了第k小的数在left~right之间
4.若这个**count**大于k,表明第k小的数在左半部分且可能包含mid,即**left=left**,** right=mid**,又保证了第k小的数在left~right之间
5.因为每次循环中都保证了第k小的数在**left~right**之间,当**left==right**时,第k小的数即被找出,等于**right**
代码
class Solution {
//二分查找
public int kthSmallest(int[][] matrix, int k) {
int row = matrix.length;
int col = matrix[0].length;
int left = matrix[0][0];
int right = matrix[row-1][col-1];
while (left < right) {
// 每次循环都保证第K小的数在start~end之间,当start==end,第k小的数就是start
int mid = (left + right) / 2;
// 找二维矩阵中<=mid的元素总个数
int count = findNotBiggerThanMid(matrix, mid, row, col);
if (count < k) {
// 第k小的数在右半部分,且不包含mid
left = mid + 1;
}else {
// 第k小的数在左半部分,可能包含mid
right = mid;
}
}
return right;
}
private int findNotBiggerThanMid(int[][] matrix, int mid, int row, int col) {
// 以列为单位找,找到每一列最后一个<=mid的数即知道每一列有多少个数<=mid
int i = 0;
int j = col-1;
int count = 0;
while (i < row && j >=0) {
if (matrix[i][j] <= mid) {
count += j+1;
i += 1;
}else {
j -= 1;
}
}
return count;
}
}
错误的集合
集合S包含从1到n的整数。不幸的是,因为数据错误,导致集合里面某一个元素复制了成了集合里面的另外一个元素的值,导致集合丢失了一个整数并且有一个元素重复。
给定一个数组nums代表了集合S发生错误后的结果。你的任务是首先寻找到重复出现的整数,再找到丢失的整数,将它们以数组的形式返回。
示例 1:
输入: nums = [1,2,2,4]
输出: [2,3]
解题思路:
-
对于寻找重复的元素:
通过将nums[Math.abs(nums[i] - 1)]的元素置负:
当某个nums[Math.abs(nums[i] - 1)]已经被置负时, nums[i]即为重复元素!
例: [4, 1, 3, 3] –> [4, 1, 3, -3] –> [-4, 1, 3, -3] –> [-4, 1, -3, -3] –> 此时n == 3, 而nums[2]已经被置负, 所以3为重复元素!
-
对于寻找缺失的元素:
缺失的元素为正数的索引+1,因为缺失元素不存在,无法对该索引的元素进行修改。
代码:
- 哈希表
class Solution {
//哈希表方法
public int[] findErrorNums(int[] nums) {
Map<Integer, Integer> map = new HashMap<>();
int dup = -1;
int miss = 1;
for (int n : nums) {
map.put(n, map.getOrDefault(n, 0) + 1);
}
for (int i = 1; i <= nums.length; i++) {
if (map.containsKey(i)) {
if (map.get(i) == 2) {
dup = i;
}
}else {
miss = i;
}
}
return new int[] {dup, miss};
}
}
- 将非重复元素变为负数
class Solution {
/*
* 遍历nums数组,在1-n数字中,如果整数i对应的nums[|i|-1]改为相反数
* 即原本为正改为负数,原本为复数改为正数。只出现一次的元素恒为负数,因此
* 重复的数字是该正数,而缺失的数字则是该索引+1
*/
public int[] findErrorNums(int[] nums) {
int dup = -1;
int miss = 1;
for(int n : nums) {
if (nums[Math.abs(n) - 1] < 0) {
dup = Math.abs(n);
}else {
nums[Math.abs(n) - 1] *= -1;
}
sum += n;
}
for (int i = 0; i < nums.length; i++) {
if (nums[i] > 0) {
miss = i +1;
}
}
return new int[] {dup, miss};
}
}
寻找重复数
给定一个包含 n + 1 个整数的数组 nums,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
示例 1:
输入: [1,3,4,2,2]
输出: 2
示例 2:
输入: [3,1,3,4,2]
输出: 3
说明:
1.不能更改原数组(假设数组是只读的)。
2.只能使用额外的 O(1) 的空间。
3.时间复杂度小于 O(n2) 。
4.数组中只有一个重复的数字,但它可能不止重复出现一次。
解题思路:
-
二分查找
我们知道二分查找要求有序,但是给定的数组不是有序的,那么怎么用二分查找呢?
原数组不是有序,但是我们知道重复的那个数字肯定是 1 到 n 中的某一个,而
1,2...,n就是一个有序序列。因此我们可以对1,2...,n进行二分查找。mid = (1 + n) / 2,接下来判断最终答案是在[1, mid]中还是在[mid + 1, n]中。我们只需要统计原数组中小于等于 mid 的个数,记为
count。如果
count > mid,鸽巢原理,在[1,mid]范围内的数字个数超过了mid,所以一定有一个重复数字。否则的话,既然不在[1,mid],那么最终答案一定在[mid + 1, n]中。 -
快慢指针+循环链表思想
详细题解见:
-
使用环形链表II的方法解题(142.环形链表II),使用 142 题的思想来解决此题的关键是要理解如何将输入的数组看作为链表。 首先明确前提,整数的数组 nums 中的数字范围是 [1,n]。考虑一下两种情况:
如果数组中没有重复的数,以数组
[1,3,4,2]为例,我们将数组下标n和数nums[n]建立一个映射关系 f(n),其映射关系n->f(n)为: 0->1 1->3 2->4 3->2 我们从下标为 0 出发,根据 f(n)f(n) 计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推,直到下标超界。这样可以产生一个类似链表一样的序列。 0->1->3->2->4->null -
如果数组中有重复的数,以数组 [1,3,4,2,2] 为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n)f(n), 其映射关系
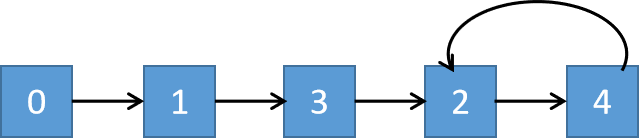
n->f(n)为: 0->1 1->3 2->4 3->2 4->2 同样的,我们从下标为 0 出发,根据 f(n)f(n) 计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推产生一个类似链表一样的序列。 0->1->3->2->4->2->4->2->…… 这里 2->4 是一个循环,那么这个链表可以抽象为下图:
从理论上讲,数组中如果有重复的数,那么就会产生多对一的映射,这样,形成的链表就一定会有环路了,
综上
- 数组中有一个重复的整数 <==> 链表中存在环
- 找到数组中的重复整数 <==> 找到链表的环入口
至此,问题转换为 142 题。那么针对此题,快、慢指针该如何走呢。根据上述数组转链表的映射关系,可推出 142 题中慢指针走一步 slow = slow.next ==> 本题 slow = nums[slow] 142 题中快指针走两步 fast = fast.next.next ==> 本题 fast = nums[nums[fast]]
-
代码
class Solution {
//二分查找
public int findDuplicate(int[] nums) {
int left = 1;
int right = nums.length-1;
int mid = (left + right) / 2;
while (left < right) {
int count = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] <= mid) {
count++;
}
}
if (count > mid) {
right = mid;
mid = (left + right) / 2;
}else {
left = mid + 1;
mid = (left + right) / 2;
}
}
return left;
}
}
class Solution {
//快慢指针
public int findDuplicate(int[] nums) {
int low = nums[0];
int fast = nums[0];
while (true) {
low = nums[low];
fast = nums[nums[fast]];
if (low == fast){
break;
}
}
fast = nums[0];
while (low != fast) {
low = nums[low];
fast = nums[fast];
}
return low;
}
}
优美的排列II
给定两个整数 n 和 k,你需要实现一个数组,这个数组包含从 1 到 n 的 n 个不同整数,同时满足以下条件:
1.如果这个数组是 [a1, a2, a3, ... , an] ,那么数组 [|a1 - a2|, |a2 - a3|, |a3 - a4|, ... , |an-1 - an|] 中应该有且仅有 k 个不同整数;.
2.如果存在多种答案,你只需实现并返回其中任意一种.
示例 1:
输入: n = 3, k = 1
输出: [1, 2, 3]
解释: [1, 2, 3] 包含 3 个范围在 1-3 的不同整数, 并且 [1, 1] 中有且仅有 1 个不同整数 : 1
示例 2:
输入: n = 3, k = 2
输出: [1, 3, 2]
解释: [1, 3, 2] 包含 3 个范围在 1-3 的不同整数, 并且 [2, 1] 中有且仅有 2 个不同整数: 1 和 2
数组的度
给定一个非空且只包含非负数的整数数组 nums, 数组的度的定义是指数组里任一元素出现频数的最大值。
你的任务是找到与 nums 拥有相同大小的度的最短连续子数组,返回其长度。
示例 1:
输入: [1, 2, 2, 3, 1]
输出: 2
解释:
输入数组的度是2,因为元素1和2的出现频数最大,均为2.
连续子数组里面拥有相同度的有如下所示:
[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]
最短连续子数组[2, 2]的长度为2,所以返回2.
示例 2:
输入: [1,2,2,3,1,4,2]
输出: 6
class Solution {
/**
* 拥有相同大小的度的最短连续子数组的首尾元素都应为拥有最大度的元素
* 因此只需要找到第一个最大度元素和最后一个元素的位置,即可计算出该子数组的长度
* 考虑使用HashMap计算元素出现次数,元素首次出现索引和最后一次出现索引
*/
public int findShortestSubArray(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
if (nums.length == 1) {
return 1;
}
Map<Integer, Integer> count = new HashMap<>();//存储元素在数组中出现次数
Map<Integer, Integer> firstIndex = new HashMap<>();//元素在数组中首次出现的索引
Map<Integer, Integer> lastIndex = new HashMap<>(); //元素在数组中最后出现的索引
for(int i = 0; i < nums.length; i++) {
int x = nums[i];
count.put(x, count.getOrDefault(x, 0) + 1);//如果元素在hashmap中未出现过,则默认值为0+1
lastIndex.put(x, i);
if (!firstIndex.containsKey(x)) {//如果hashmap中不含元素x,则首次出现的索引为i,如果包含则不更新
firstIndex.put(x, i);
}
}
//统计最大度为多少
int max = 0;
for(int num : nums) {
if (count.get(num) > max) {
max = count.get(num);
}
}
//拥有相同度数的元素可能有多个,因此要比较他们的连续子数组的大小
int shortestLen = nums.length;
for(int num : nums) {
if (count.get(num) == max) {
int len = lastIndex.get(num) - firstIndex.get(num) + 1;
if (len < shortestLen) {
shortestLen = len; //相同最大度元素中连续子数组最短的长度
}
}
}
return shortestLen;
}
}
托普利茨矩阵
如果矩阵上每一条由左上到右下的对角线上的元素都相同,那么这个矩阵是 托普利茨矩阵 。
给定一个 M x N 的矩阵,当且仅当它是托普利茨矩阵时返回 True。
示例 1:
输入:
matrix = [
[1,2,3,4],
[5,1,2,3],
[9,5,1,2]
]
输出: True
解释:
在上述矩阵中, 其对角线为:
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]"。
各条对角线上的所有元素均相同, 因此答案是True。
示例 2:
输入:
matrix = [
[1,2],
[2,2]
]
输出: False
解释:
对角线"[1, 2]"上的元素不同。
class Solution {
/**.
* 检查相邻右上元素
* 若矩阵从左上到右下的对角线元素相等,那么我们可以得出规律:
* 矩阵中任意元素若上方和右方有相邻元素时,相邻元素相等,则为托普利茨矩阵
* 因此遍历时,除去第一行和最后一列进行遍历
*/
public boolean isToeplitzMatrix(int[][] matrix) {
for (int i = 0; i < matrix.length; i++) {
for(int j = 0; j < matrix[0].length; j++) {
if (i > 0 && j < matrix[0].length - 1 && matrix[i - 1][j] != matrix[i][j + 1]) {
return false;
}else{
continue;
}
}
}
return true;
}
}
数组嵌套
索引从0开始长度为N的数组A,包含0到N - 1的所有整数。找到最大的集合S并返回其大小,其中 S[i] = {A[i], A[A[i]], A[A[A[i]]], ... }且遵守以下的规则。
假设选择索引为i的元素A[i]为S的第一个元素,S的下一个元素应该是A[A[i]],之后是A[A[A[i]]]... 以此类推,不断添加直到S出现重复的元素。
示例 1:
输入: A = [5,4,0,3,1,6,2]
输出: 4
解释:
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.
其中一种最长的 S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}
class Solution {
/**
* n长度的数组中包含0-n-1的不重复数字,取出一个数字以当前数字作为下一个数字的下标,
* 可以看出按此逻辑取出的数字最终会构成一个圆环,剩下的数字也如此能构成圆环,找最长的序列,就是找最大的圆环。
* 因此,题目可以转换为,一个图中存在一个或多个圆环,求其中最大的圆环长度。从圆环中的任意元素出发所得的结果相同。
*
* 操作:遍历数组,将数组值作为嵌套数组的下标,并将遍历过的值赋为-1
*/
public int arrayNesting(int[] nums) {
int res = 0;
for (int i = 0; i < nums.length; i++) {
int count = 0;
int index = i;
while (nums[index] != -1){
count++;
int tmp = nums[index];
nums[index] = -1;
index = tmp;
}
res = Math.max(count, res);
}
return res;
}
}
- 原文作者:jchen
- 原文链接:http://jchenTech.github.io/post/Leetcode/%E6%95%B0%E7%BB%84%E4%B8%8E%E7%9F%A9%E9%98%B5/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。