雾霾是由空气中的灰尘和烟雾等小的漂浮颗粒产生的常见大气现象。这些漂浮的颗粒极大地吸收和散射光，导致图像质量下降。在雾霾影响下，视频监控，远程感应，自动驾驶等许多实际应用很容易受到威胁，检测和识别等高级计算机视觉任务很难完成。因此，图像去雾（除雾）成为一种越来越重要的技术。在图像去雾领域，不得不学习何凯明在2009CVPR上获最佳论文的文章。

Dark Channel Prior

1 暗通道先验理论

暗通道先验是基于如下观察，在户外的无雾图像中，在大部分非天空区域，至少有一个通道值是很小一个数或趋近于零。因此，对任意一幅图 $J$，给出暗通道 $J^{dark}$ 的表示：

其中两个最小是各通道最小，局部窗口最小。即首先对图像每个像素取三通道中最小值，得到一个单通道图，然后对这个单通道图作最小值滤波就可以得到暗通道图 $J^{dark}$。

作者将造成这个现象的原因归结为以下三点：

  • 各类物体的阴影，玻璃
  • 彩色物体表面，如花草树木，蓝色的水面
  • 色物体表面，如树干，石头等

正因为自然界总是充满了彩色和阴影，就导致了图像暗通道总是很暗。为了验证这个先验知识，作者统计了大量图片，发现基本都符合这个先验。以下是几幅680*1024的风景图在不同大小滤波窗口下的暗通道图：

暗通道先验示例图

以上图像基本都符合暗通道先验，由此可见暗通道的普遍性。在暗通道先验的基础上，就可以进行去雾算法的推导。

2 大气散射模型

在计算机视觉和计算机图形领域，一个常用来描述有雾图像的公式表达为：

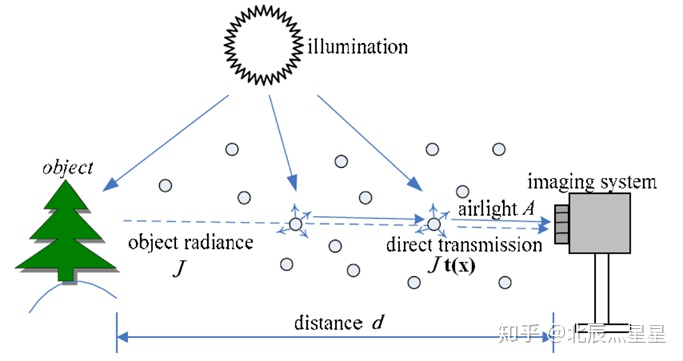
其中: $I(x)$ 为拍摄的含雾图像，$J(x)$ 为无雾图像，$t(x)$ 为透射率，用来描述太阳光通过媒质投射到照相机过程中没有被散射的部分，$A$ 为全球大气光成分。

可见含雾图像 $I(x)$ 的形成主要由两部分决定：第一部分是 $I(x)t(x)$ 构成的直接衰减项，用于描述景物光线在透射媒介中经衰减后的部分；第二部分是 $A[1-t(x)]$ 构成的大气光照，它由图像采集装置前方的散射引起，会导致景物色调的偏移。如图所示。

大气散射模型

3 暗通道先验去雾算法

首先假设大气光成分 $A$ 已知。去雾模型可以化为以下方程：

$$ \frac{{{I^c}(x)}}{{{A^c}}}{\text{ = }}t(x)\frac{{{J^c}(x)}}{{{A^c}}}{\text{ + }}1 - t(x) $$

上标 $c$ 即表示r,g,b三通道。

进一步假设每个滤波窗口内的透射率 $t(x)$ 是常数，记为$\overline t (x)$ ，然后对方程两边同时计算暗通道，即作两次最小值运算，可得下式：

因为 $\bar t(x)$ 是常量，所以放在最小运算外面。

根据暗通道先验，$J$ 趋近于零：

因为 $A^c$ 总是正值，可得：

代回原式，即可简单地得到透射率估计值：

同时，即使是晴天，大气光成分还是存在的，尤其是在看远处的物体时给人的感觉更强。这种大气光成分会给人一种景深的层次感，去雾要有所保留。因此，引入一个常量参数 $\omega (0 < \omega < 1)$ 用来控制去雾的程度：

作者在文中建议的 $\omega$ 为0.95。

在算法开始的地方就假设 $A$ 是已知，那么具体如何得到 $A$ 的值。作者在文中给出的方法是，在暗通道中找出前0.1%最亮的点，即透射率最小的点。对于这些点，去雾图中找到对于的点，并取它们中的所有通道最大的值作为 $A$ 的近似。至此，透射率 $t(x)$，大气光成分 $A$，雾图 $I$，都是已知了，就可以求解无雾图：

其中，$t_0$ 为一个透射率下界。由于直接恢复时，当透射率 $t(x)$ 接近零的时候，$J(x)t(x)$ 也为零，这就会失去原图信息，容易引入噪声，因此设置一个下界，在雾密度很大的地方，保留一定数量的雾。$t_0$ 的值一般取0.1。作者还提到，去雾后的图像一般会显得比较暗淡，可以适当增加曝光以得到更好的效果。

参考文章