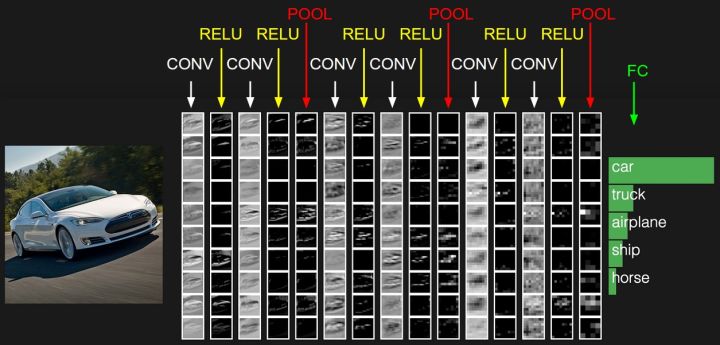
卷积神经网络（CNN）是一种深层神经网络，已被证明在计算机视觉任务中表现出色，例如图像分类，目标检测，目标定位和神经样式转换。 在这篇文章中，我将详细地介绍构成卷积神经网络的不同层：卷积层，池化层和完全连接层。

卷积神经网络实例-汽车图像识别

1 前言——卷积神经网络介绍

1.1 为什么不用全连接神经网络？

如果用全连接神经网络处理大尺寸图像具有三个明显的缺点：

  • 首先将图像展开为向量会丢失空间信息；
  • 其次参数过多效率低下，训练困难；
  • 同时大量的参数也很快会导致网络过拟合。

而使用卷积神经网络可以很好地解决上面的三个问题。

1.2 卷积神经网络

卷积神经网络的真谛：

卷积神经网络主要由两部分组成 一部分是特征提取（卷积、激活函数、池化），另一部分是分类识别（全连接）

如今，CNN被用来应用于各个领域，比如物体分割、风格转换、自动上色……

————但是，CNN真正能做的，只是起到一个图像特征提取器的作用！

1.3 引子：边界检测

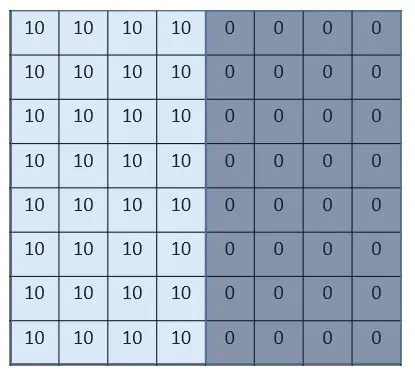
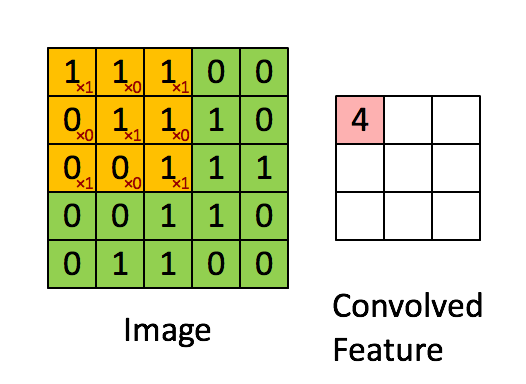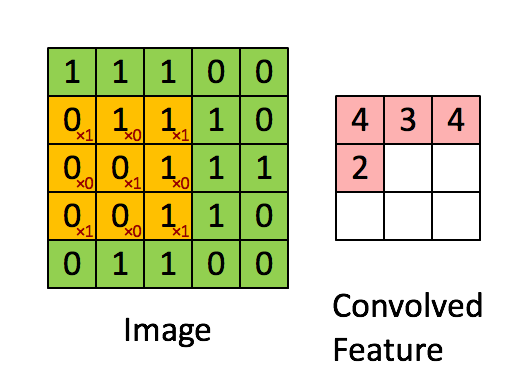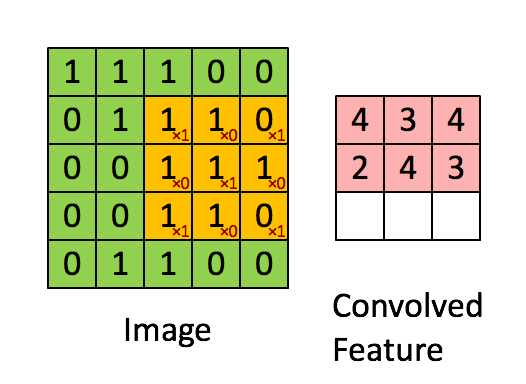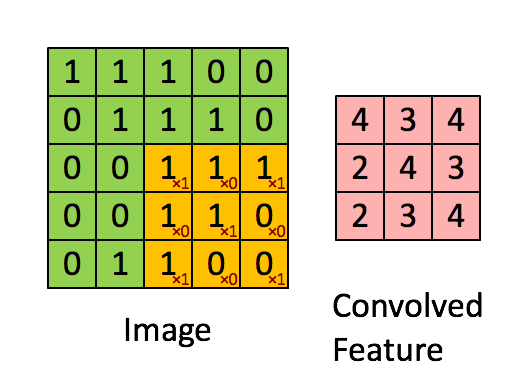
我们来看一个最简单的例子：“边界检测（edge detection）”，假设我们有这样的一张图片，大小8×8：

边界检测

图片中的数字代表该位置的像素值，我们知道，像素值越大，颜色越亮，所以为了示意，我们把右边小像素的地方画成深色。图的中间两个颜色的分界线就是我们要检测的边界。

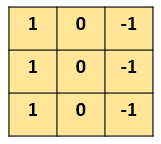
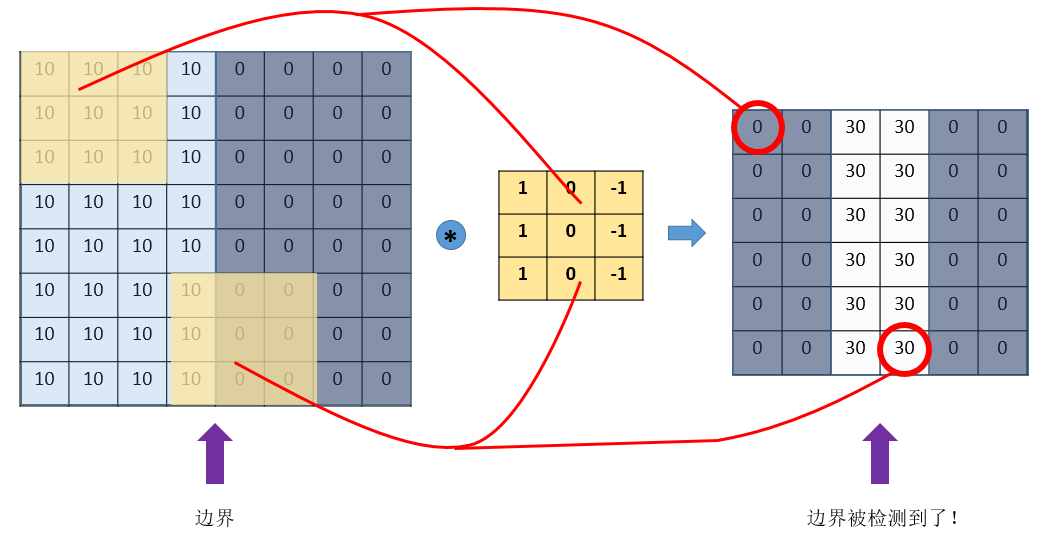
怎么检测这个边界呢？我们可以设计这样的一个 滤波器（filter，也称为kernel），大小3×3：

滤波器

然后，我们用这个filter，往我们的图片上“盖”，覆盖一块跟filter一样大的区域之后，对应元素相乘，然后求和。计算一个区域之后，就向其他区域挪动，接着计算，直到把原图片的每一个角落都覆盖到了为止。这个过程就是 “卷积”。

（我们不用管卷积在数学上到底是指什么运算，我们只用知道在CNN中是怎么计算的。）

这里的“挪动”，就涉及到一个步长了，假如我们的步长是1，那么覆盖了一个地方之后，就挪一格，容易知道，总共可以覆盖6×6个不同的区域。

那么，我们将这6×6个区域的卷积结果，拼成一个矩阵：

边界检测过程

诶？！发现了什么？ 这个图片，中间颜色浅，两边颜色深，这说明咱们的原图片中间的边界，在这里被反映出来了!

从上面这个例子中，我们发现，我们可以通过设计特定的filter，让它去跟图片做卷积，就可以识别出图片中的某些特征，比如边界。

上面的例子是检测竖直边界，我们也可以设计出检测水平边界的，只用把刚刚的filter旋转90°即可。对于其他的特征，理论上只要我们经过精细的设计，总是可以设计出合适的filter的。

我们的CNN（convolutional neural network），主要就是通过一个个的filter，不断地提取特征，从局部的特征到总体的特征，从而进行图像识别等等功能。

那么问题来了，我们怎么可能去设计这么多各种各样的filter呀？首先，我们都不一定清楚对于一大推图片，我们需要识别哪些特征，其次，就算知道了有哪些特征，想真的去设计出对应的filter，恐怕也并非易事，要知道，特征的数量可能是成千上万的。

其实学过神经网络之后，我们就知道，这些filter，根本就不用我们去设计，每个filter中的各个数字，不就是参数吗，我们可以通过大量的数据，来 让机器自己去“学习”这些参数嘛。这，就是CNN的原理。

2 卷积神经网络结构

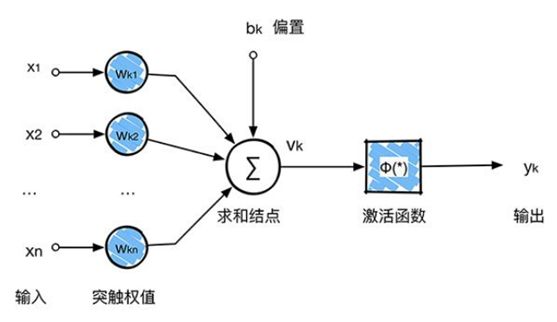
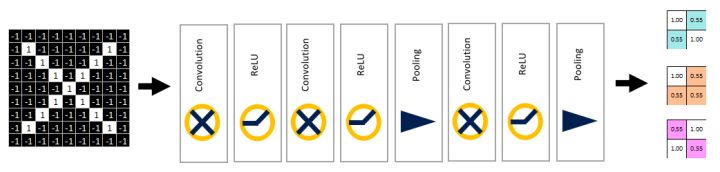
卷积神经网络主要由这几类层构成：输入层、卷积层，ReLU层、池化（Pooling）层和全连接层（全连接层和常规神经网络中的一样）。通过将这些层叠加起来，就可以构建一个完整的卷积神经网络。在实际应用中往往将卷积层与ReLU层共同称之为卷积层，所以卷积层经过卷积操作也是要经过激活函数的。具体说来，卷积层和全连接层（CONV/FC）对输入执行变换操作的时候，不仅会用到激活函数，还会用到很多参数，即神经元的权值w和偏差b；而ReLU层和池化层则是进行一个固定不变的函数操作。卷积层和全连接层中的参数会随着梯度下降被训练，这样卷积神经网络计算出的分类评分就能和训练集中的每个图像的标签吻合了。

2.1 卷积层

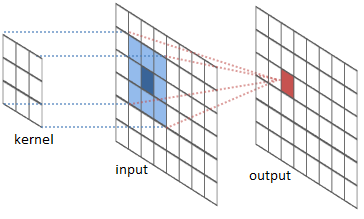
卷积层对输入图像进行转换，以从中提取特征。在这种转换中，图像与内核（或滤波器）卷积。

图像卷积

核是一个小的矩阵，其高度和宽度小于要卷积的图像。 它也被称为卷积矩阵或卷积掩码。 该核在图像输入的高度和宽度上滑动，并且核的点积和图像在每个空间位置处进行计算。 籽粒滑动的长度称为步幅长度。 在下面的图像中，输入图像的大小为5X5，内核的大小为3X3，步幅为1。输出图像也称为卷积特征。

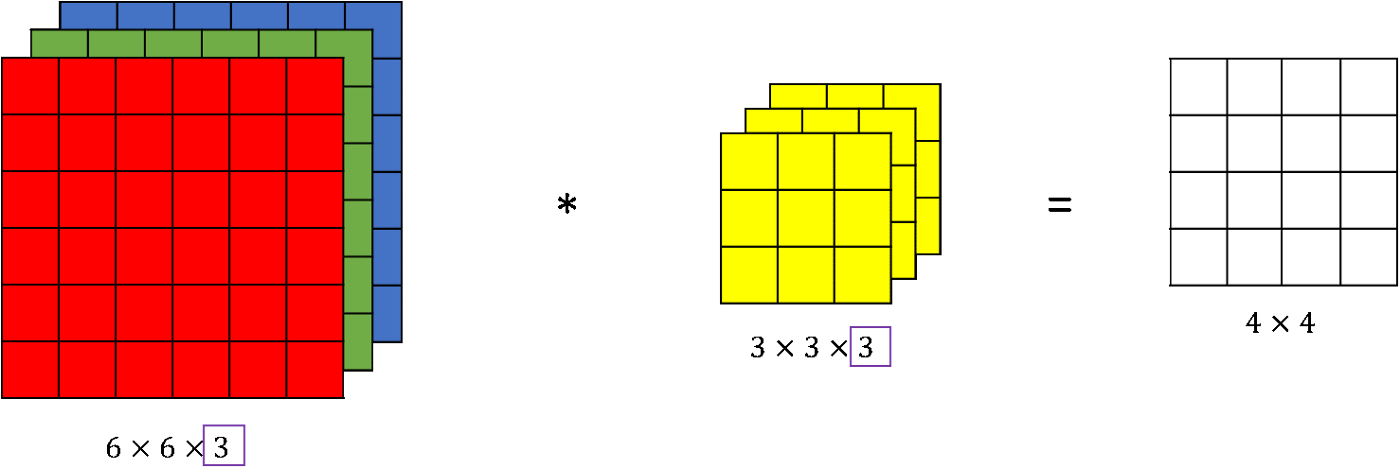
单通道图像卷积过程

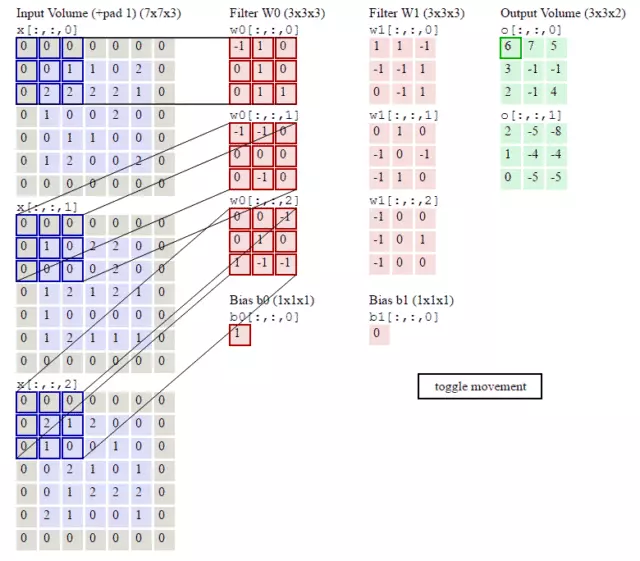
当使用通道3卷积彩色图像（RGB图像）时，滤镜的通道也必须为3。 换句话说，在卷积中，内核中的通道数必须与输入图像中的通道数相同。

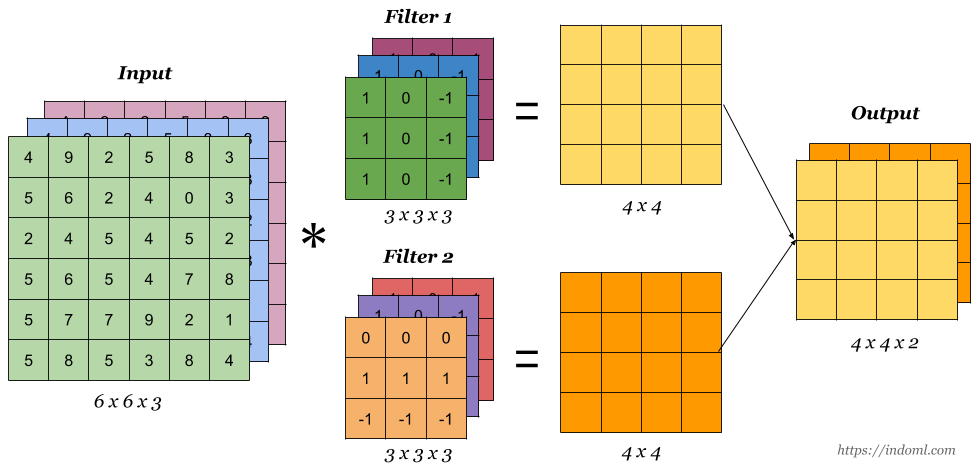
RGB图像卷积过程

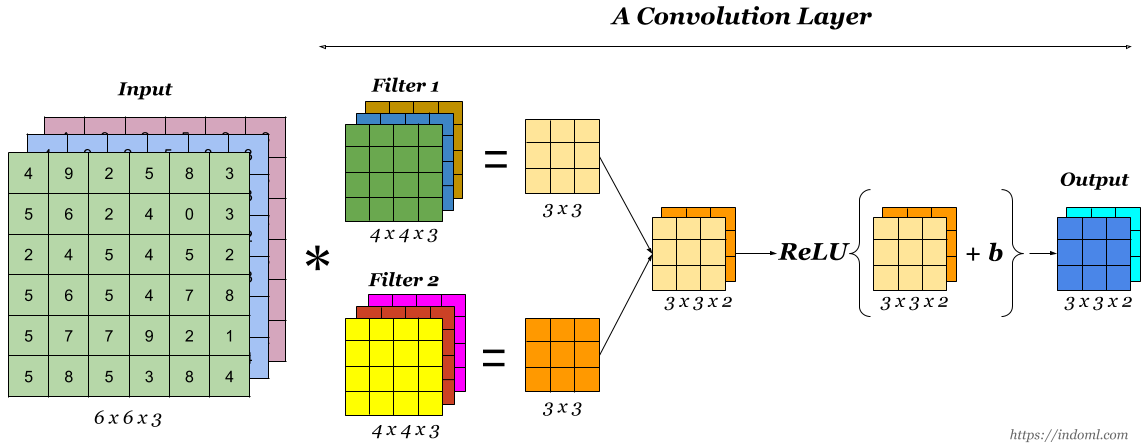
当我们想使用卷积从一个图像中提取多个特征时，我们可以使用多个内核而不是仅使用一个。 在这种情况下，所有内核的大小必须相同。 输入图像和输出图像的卷积特征一个接一个地堆叠在一起以创建输出，因此通道数等于使用的滤波器个数。 请参阅下图以供参考。

多个内核或滤波器的卷积过程

更具体的是，在加入偏置bias之后，每个filter对应每个通道有一组w权重，一个filter滑动到一个位置后计算三个通道的卷积，求和，加bias，得到这个filter在该位置的最终结果，每个filter的输出是各个通道的汇总。请参阅下图以供参考：

加入bias的多滤波器卷积计算

2.2 非线性激活层——重点理解激活函数ReLu

2.2.1什么是ReLu

官方解释：

卷积层对原图运算多个卷积，产生一组线性激活响应，而非线性激活层是对之前的结果进行一个非线性的激活响应。

激活函数的作用是用来加入非线性因素，把卷积层输出结果做非线性映射。

激活函数作用过程

在卷积神经网络中用到最多的非线性激活函数是Relu函数，

它的公式定义：f(x)=max(0,x)

即，保留大于等于0的值，其余所有小于0的数值直接改写为0,>=0的值全部保持不变：

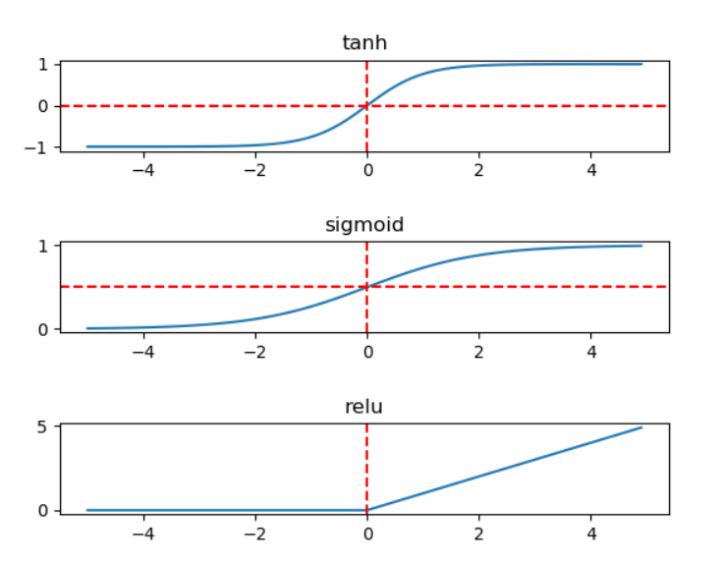
ReLu激活函数作用结果

2.2.2 常见的激活函数——sigmoid、tanh和relu三种非线性函数

三种非线性激活函数特征

隐藏层:

tanh函数要优于sigmoid函数，优势在于其取值范围介于-1 ~ 1之间，数据的平均值为0，而不像sigmoid为0.5，有类似数据中心化的效果。 可以认为是sigmoid的平移版本，

输出层:

sigmoid也许会优于tanh函数，原因在于你希望输出结果的概率落在0 ~ 1 之间，比如二元分类，sigmoid可作为输出层的激活函数。

实际应用中，特别是深层网络在训练时:

tanh和sigmoid会在端值趋于饱和，造成训练速度减慢，故深层网络的激活函数默认大多采用relu函数，浅层网络可以采用sigmoid和tanh函数。

那么为什么现在这么多网络，都更多地使用ReLU函数呢？

一个重要原因就是上面提到的，其稀疏激活性。

1、标准的sigmoid函数输出不具备稀疏性，需要用一些惩罚因子来训练出一大堆接近0的冗余数据来，从而产生稀疏数据

2、而ReLU是线性修正。它的作用是如果计算出的值小于0，就让它等于0，否则保持原来的值不变。

这是一种简单粗暴地强制某些数据为0的方法，然而经实践证明，训练后的网络完全具备适度的稀疏性。而且训练后的可视化效果和传统方式预训练出的效果很相似，这也说明了ReLU具备引导适度稀疏的能力。

因此，ReLu的使用，使得网络可以自行引入稀疏性，同时大大地提高了训练速度。

激活函数是卷积层的最后一个组成部分，可增加输出中的非线性。通常，在卷积层中将ReLu函数或Tanh函数用作激活函数。 这是一个简单卷积层的图像，其中将6X6X3输入图像与大小为4X4X3的两个内核卷积以得到大小为3X3X2的卷积特征，对其应用激活函数以获取输出，这也称为特征地图feature map。

一个卷积层

2.3 池化层pooling

2.3.1 池化的作用

（1）卷积操作后，我们得到了一张张有着不同值的feature map，尽管数据量比原图少了很多，但还是过于庞大（深度学习动不动就几十万张训练图片），这时候该怎么办？？

池化操作，最大的作用就是减少数据量。

池化层的引入，是仿照人的视觉系统对视觉输入对象进行降维和抽象。

（2）【官方说明】在卷积神经网络过去的工作中，研究者普遍认为池化层有如下三个功效：

1、特征不变形：池化操作使得模型更加关注是否存在某些特征，而不是特征具体的位置。

2、特征降维：池化相当于在空间范围内做了维度约减，从而使模型可以抽取更加广范围的特征。同时减小了下一层的输入大小，进而减少计算量和参数个数。

3、在一定程度上防止过拟合，更方便优化。 （由1、2可知，这种池化机制能够有效地原因在于，在发现一个特征之后，它的精确位置远不及它和其他特征的相对位置的关系重要。池化层会不断地减小数据的空间大小，因此参数的数量和计算量也会下降，这在一定程度上也控制了过拟合。）

2.3.2 池化的分类

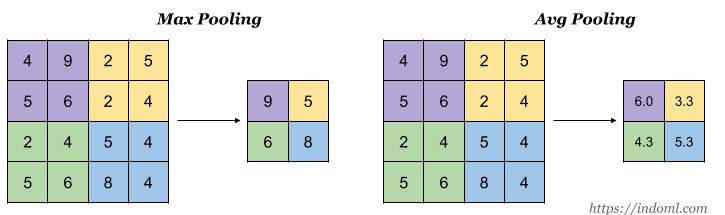
池操作也使用内核和跨步。 在下面的示例图像中，使用2X2滤波器合并大小为4，跨度为2的4X4输入图像。

有不同类型的池。 最大池和平均池是卷积神经网络中最常用的池方法。

最大池化：在最大池化中，从要素图的每个面片中选择最大值以创建缩小图。

平均池化：在平均池化中，从要素图的每个面片中选择平均值以创建缩小图。

最大池化和平均池化

2.3.3 总结

因为最大池化保留了每一个小块内的最大值，所以它相当于保留了这一块最佳匹配结果。

这也就意味着：池化操作不会具体关注窗口内到底是哪一个地方匹配了，而只关注是不是有某个地方匹配上了。

侧面说明——CNN能够发现图像中是否具有某种特征，而不用在意到底在哪里具有这种特征。这也就帮助解决，之前提到的计算机逐一像素匹配的死板做法。

到这里就介绍了CNN的基本配置—卷积层、Relu层、池化层。

在常见的几种CNN中，这三层都是可以堆叠使用的，将前一层的输入作为后一层的输出。

比如：

堆叠卷积激活与池化层

2.4 全连接层

2.4.1 全连接层的作用

  1. 为什么是全连接？

卷积取的是局部特征，全连接就是把以前的局部特征重新通过权值矩阵，组装成完整的图，因为用到了所有的局部特征，所以叫全连接。

  1. 全连接层要做的，是什么？

起到“分类”的作用

全连接层要做的，就是对之前的所有操作进行一个总结。对特征图进行维度上的改变，来得到每个分类类别对应的概率值。

2.4.2 全连接操作

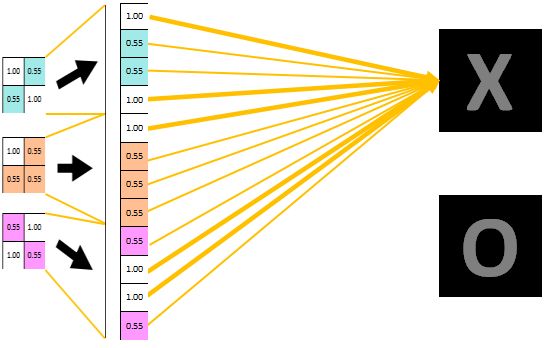
完全连接的层位于卷积神经网络的末端。 由较早层产生的特征图将展平为矢量。然后，此向量被馈送到完全连接的层，以便它捕获高级要素之间的复杂关系。该层的外面是一维特征向量。

（1）接着上面的例子，原图片尺寸为9X9，在一系列的卷积、relu、池化操作后，得到尺寸被压缩为2X2的三张特征图。

得到了2X2的特征图后，对其应用全连接网络，再全连接层中有一个非常重要的函数——Softmax，它是一个分类函数，输出的是每个对应类别的概率值。

比如：【0.5，0.03，0.89，0.97，0.42，0.15】就表示有6个类别，并且属于第四个类别的概率值0.97最大，因此判定属于第四个类别。

（2）将三个特征图改变维度直接变成一维的数据，展开的数据即为属于类别X的概率值，值大小也在对应X的线条粗细中表现出来了。

全连接层分类

现在，您知道什么是卷积神经网络以及组成卷积神经网络的不同层，即卷积层，池化层和完全连接的层。

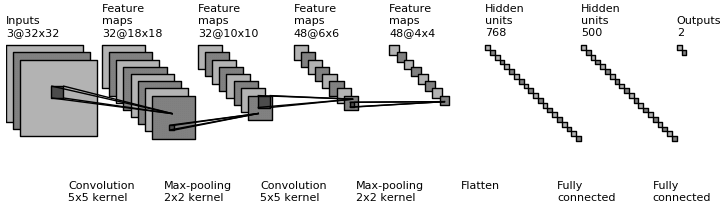
下面是用于二进制图像分类的卷积神经网络的简单架构。该网络将两个不同类别之间的输入分类。 该网络接收大小为32x32x3的RBG图像，输出大小为2（等于分类的类数）。 该网络的第一层是具有5x5x3内核的卷积层，第二层是具有2x2内核大小的最大池化层，第三层是具有5x5x3内核的卷积层，第四层是最大池化层 如果内核大小为2x2，则将输出展平为一个向量，并馈入最后两个都是完全连接的层。

用于二进制图像分类的CNN的简单架构

3 CNN中一些基本概念

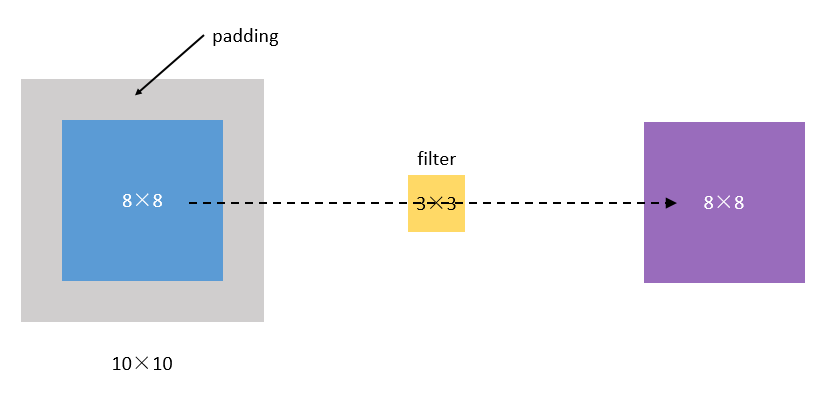
  1. padding 填白 从上面的引子中，我们可以知道，原图像在经过filter卷积之后，变小了，从(8,8)变成了(6,6)。假设我们再卷一次，那大小就变成了(4,4)了。

这样有啥问题呢？ 主要有两个问题：

  • 每次卷积，图像都缩小，这样卷不了几次就没了；
  • 相比于图片中间的点，图片边缘的点在卷积中被计算的次数很少。这样的话，边缘的信息就易于丢失。

为了解决这个问题，我们可以采用padding的方法。我们每次卷积前，先给图片周围都补一圈空白，让卷积之后图片跟原来一样大，同时，原来的边缘也被计算了更多次。

padding填白

比如，我们把(8,8)的图片给补成(10,10)，那么经过(3,3)的filter之后，就是(8,8)，没有变。

我们把上面这种“让卷积之后的大小不变”的padding方式，称为 **“Same”**方式， 把不经过任何填白的，称为 **“Valid”**方式。这个是我们在使用一些框架的时候，需要设置的超参数。

  1. stride 步长

前面我们所介绍的卷积，都是默认步长是1，但实际上，我们可以设置步长为其他的值。

比如，对于(8,8)的输入，我们用(3,3)的filter， 如果stride=1，则输出为(6,6); 如果stride=2，则输出为(3,3);（这里例子举得不大好，除不断就向下取整）

4 卷积神经网络 VS. 传统神经网络

其实现在回过头来看，CNN跟我们之前学习的神经网络，也没有很大的差别。

传统的神经网络，其实就是多个FC层叠加起来。 CNN，无非就是把FC改成了CONV和POOL，就是把传统的由一个个神经元组成的layer，变成了由filters组成的layer。

那么，为什么要这样变？有什么好处？ 具体说来有两点：

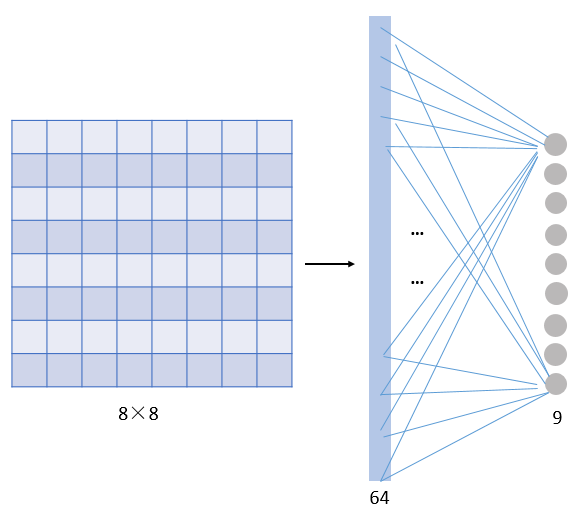
  1. 参数共享机制（parameters sharing） 我们对比一下传统神经网络的层和由filters构成的CONV层： 假设我们的图像是8×8大小，也就是64个像素，假设我们用一个有9个单元的全连接层：

全连接神经网络参数个数

那这一层我们需要多少个参数呢？需要 64×9 = 576个参数（先不考虑偏置项b）。因为每一个链接都需要一个权重w。

那我们看看 同样有9个单元的filter是怎么样的：

CNN参数个数

其实不用看就知道，有几个单元就几个参数，所以总共就9个参数！

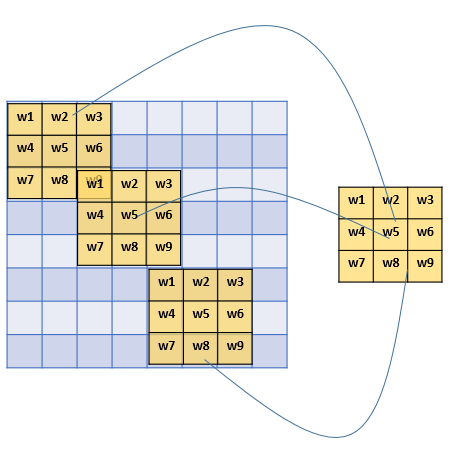
因为，对于不同的区域，我们都共享同一个filter，因此就共享这同一组参数。

这也是有道理的，通过前面的讲解我们知道，filter是用来检测特征的，那一个特征一般情况下很可能在不止一个地方出现，比如“竖直边界”，就可能在一幅图中多出出现，那么 我们共享同一个filter不仅是合理的，而且是应该这么做的。

由此可见，参数共享机制，让我们的网络的参数数量大大地减少。这样，我们可以用较少的参数，训练出更加好的模型，典型的事半功倍，而且可以有效地 避免过拟合。

同样，由于filter的参数共享，即使图片进行了一定的平移操作，我们照样可以识别出特征，这叫做** “平移不变性”**。因此，模型就更加稳健了。

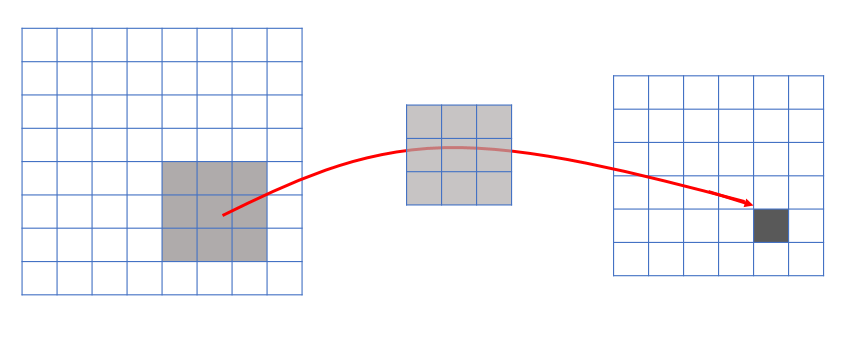
2.连接的稀疏性（sparsity of connections）

由卷积的操作可知，输出图像中的任何一个单元，只跟输入图像的一部分有关系。

连接的稀疏性

而传统神经网络中，由于都是全连接，所以输出的任何一个单元，都要受输入的所有的单元的影响。这样无形中会对图像的识别效果大打折扣。比较，每一个区域都有自己的专属特征，我们不希望它受到其他区域的影响。

正是由于上面这两大优势，使得CNN超越了传统的NN，开启了神经网络的新时代。

5 案例学习

下面是卷积神经网络领域中比较有名的几种结构：

  • LeNet ，第一个成功的卷积神经网络应用，是Yann LeCun在上世纪90年代实现的。当然，最著名还是被应用在识别数字和邮政编码等的LeNet结构。

  • AlexNet ，AlexNet卷积神经网络在计算机视觉领域中受到欢迎，它由Alex Krizhevsky，Ilya Sutskever和Geoff Hinton实现。AlexNet在2012年的ImageNet ILSVRC 竞赛中夺冠，性能远远超出第二名（16%的top5错误率，第二名是26%的top5错误率）。这个网络的结构和LeNet非常类似，但是更深更大，并且使用了层叠的卷积层来获取特征（之前通常是只用一个卷积层并且在其后马上跟着一个汇聚层）。

  • ZF Net ，Matthew Zeiler和Rob Fergus发明的网络在ILSVRC 2013比赛中夺冠，它被称为 ZFNet（Zeiler & Fergus Net的简称）。它通过修改结构中的超参数来实现对AlexNet的改良，具体说来就是增加了中间卷积层的尺寸，让第一层的步长和滤波器尺寸更小。

  • GoogLeNet ，ILSVRC 2014的胜利者是谷歌的Szeged等实现的卷积神经网络。它主要的贡献就是实现了一个奠基模块，它能够显著地减少网络中参数的数量（AlexNet中有60M，该网络中只有4M）。还有，这个论文中没有使用卷积神经网络顶部使用全连接层，而是使用了一个平均汇聚，把大量不是很重要的参数都去除掉了。GooLeNet还有几种改进的版本，最新的一个是Inception-v4。

  • VGGNet ，ILSVRC 2014的第二名是Karen Simonyan和 Andrew Zisserman实现的卷积神经网络，现在称其为VGGNet。它主要的贡献是展示出网络的深度是算法优良性能的关键部分。他们最好的网络包含了16个卷积/全连接层。网络的结构非常一致，从头到尾全部使用的是3x3的卷积和2x2的汇聚。他们的预训练模型是可以在网络上获得并在Caffe中使用的。VGGNet不好的一点是它耗费更多计算资源，并且使用了更多的参数，导致更多的内存占用（140M）。其中绝大多数的参数都是来自于第一个全连接层。后来发现这些全连接层即使被去除，对于性能也没有什么影响，这样就显著降低了参数数量。

  • ResNet ，残差网络（Residual Network）是ILSVRC2015的胜利者，由何恺明等实现。它使用了特殊的跳跃链接，大量使用了批量归一化（batch normalization）。这个结构同样在最后没有使用全连接层。读者可以查看何恺明的的演讲（视频，PPT），以及一些使用Torch重现网络的实验。ResNet当前最好的卷积神经网络模型（2016年五月）。何开明等最近的工作是对原始结构做一些优化，可以看论文Identity Mappings in Deep Residual Networks，2016年3月发表。

参考文章：